ISUCON12予選にチーム Takedashi として参加し、予選通過しました (52957点)
2022-07-23のISUCON12予選にチーム Takedashiとして参加して、52957点で予選通過しました。 予選通過はISUCON8以来だと思います。その間に子供が二人産まれており、時間の流れを感じますね。
リポジトリはこちら github.com
メンバーの @chibieggも記事を書いているのでこちらもどうぞ http://blog.chibiegg.net/2022/07/24_15_864.htm
メンバーはいつもの
| アイコン | メンバー | 役割 |
|---|---|---|
 |
chibiegg | インフラ/デプロイ/プルリク管理/データ整備/コーディング |
 |
__math | 司令塔/コードリーディング/コーディング |
 |
misodengaku | コードリーディング/ミドルウェアチューニング/コーディング |
となっています。今回は絵に描いたように上手に物事を進められたのがよかったです、100点満点!
スコア推移: 
司令塔の動き方
他の2人と話し合ったわけではないのですが、今年は勝手に自分の動き方を変えていました。スクラム開発?
リスクマネジメントを最も重要視しました 具体的には以下の3つの項目を頭の中で比較して、改善内容をチームの人にお願いしていました。
- リスク : 実装の難易度、手戻りが発生する確率、実装が失敗した時のrevertは容易か
- 費用 : 実装からベンチマーク実行終了の合計時間。 実装が20分、デプロイ1分、ベンチマークが2分なら23分
- 効果 : 実装後のベンチスコアの上昇割合。 1000 -> 1500 なら 1.5倍
これらをベースに優先度を付けます。 リスク、費用は個人の特性や実装内容で変わるので難しいですね。
我々のチームは何回か本選に出場したことがあるので、スコアの安定感を高めることが出来れば予選突破の安定するだろうと思いリスクを取りすぎないようにしました。 長年固定メンバーで色々な大会に出ていると、各々の得意分野、実装時間の見積もりの精度が上がって良いですね。毎年違うメンバーで出る場合はこのあたりの戦略が変わるだろうなと思います。
改善点の見つけ方
ボトルネック以外は目をつむる、これに尽きます。 優先順位は
- 各種メトリクスを見る
- アプリケーションで遊んで仕様を一通り確認する
- 規約とかを読む
- コードを読む
です。
最序盤はメトリクスが出揃ってないので、その間に規約やコードを読んだりしておくといいかと思います。コードを読むのが一番優先度が低い理由ですが、自分はほっといたらコード読んでるのでわざと優先度を下げてます。
実装方針の伝え方
序盤は改善点が大量にあるので、見つけた改善点、気づきをGoogle Docにまとめてチームの人に見せていました。 中盤後半は手が打てる数点しかないのと、slack + 脳内だけで整理しきれるのでdocには残してません オフラインならホワイトボードでいいんですけどね…

本番時系列
9:00 本番前
vscodeとgolangをubuntuに入れたり、公開鍵がちゃんとgithubに登録されてるか確認したり…
10:00 競技開始
- @chibiegg : CloudFormationでプロビジョニング開始
- @misodengaku, __math: 規約とかを読んでる
10:10 初回ベンチマーク
- インスタンスが立ったのでとりあえずベンチを走らせる
- @chibiegg: コードをprivate repoに上げる
- @chibieggと@misodengakuにpprofとかnginxのログ、mysqlのスローログとかを取れるようにお願いする
10:?? アプリを試す、コードを眺める
- MySQLとSQLiteが併用されていることに気づく。各tenant毎にsqliteのdbファイルが切られているが、各クエリに
tenantId = ?という文字があるので、マージできそうだなと漠然と考えていた。 とりあえず MySQLをisuportsと別サーバに移動
dispenseIDという、"admin" MySQLに依存したID発行関数があり、uuidに変えようか迷ったものの、まだ読んでない箇所もあるのでコードリーディングを続行。
11:00 nginxのログからボトルネックの確認
^/api/player/competition/[id]/ranking ^/api/player/player/[^/]+$
の2つのエンドポイントが遅いことがわかる。visit_history以外のMySQLの負荷は低いので、go+SQLiteのisuportsのIO waitかCPUだろうとあたりを付けて、この辺のコードを読み込む。
* sqliteのテーブル構造と、特にplayer_score tableの使われ方を把握する。
11:00 visit_historyの改善
- @chibiegg にとりあえず visit_history のindexを貼ってもらう。MySQLの負荷が大幅に下がり、go + sqliteの負荷がボトルネックになることを確認。
現在2台構成 (go+sqlite, mysql)で、go+sqliteのCPUが張り付いていたので、
dispenseIDはとりあえず放置決定に。
11:xx player_scoreの改善
player_scoreのレコード量が減らせることに気づいたものの、ここで間違ってたら手戻りがひどいため他の人と理解が正しいかダブルチェックしてもらう。- 各(
tenantId, competitionId)毎に、同じプレイヤーのレコードは1つまでしか必要ないことがわかったので、2つの事をしたくなった- SQLiteのデータ量を減らす
- 初期データをいじるので少しリスクが大きめ
competitionScoreHandlerでinsertするデータ量を減らす- 間違っていてもinitializeすれば容易にデータが戻せる
- SQLiteのデータ量を減らす
ということでまず後者を実装してもらう : github.com
ベンチが通ったので、前者の処理をしても大丈夫そうだと確証が取れる。
11:xx SQLite -> MySQL
作業は2段階に分けた。
分けた理由: * "merge"が完了するだけでコードの見通しが良くなり、複数テナントにまたがるSQLの実行回数が1回になる。IOもCPU使用率も減りそう * "merge"をするだけでいちいちconnectionをopen, closeしているコードが全部消える。現状のままでconnectionを貼り続けるコードにするのはバグりやすそう * "migration"に失敗しても手戻りがほとんど発生しないのでリスクが低い
ふたりとも忙しそうだし、__mathが一部担当。 chibieggの手が空いたら交代してもらうことに。
12:10 細々とした改善
competitionScoreHandlerはBulk Insertに出来る。実装は軽いしバグりにくそう、将来ボトルネックになりそう、ということで @chibiegg にやってもらう。 github.com- @misodengakuに引き続きpprof周りをいい感じにやってもらう。
- sqliteのmergeを行っている。dumpは一瞬だったがdump後1つのDBに流しこむのに時間がかかる。
- 1.dbをコピーして、それに2~99.dbの中身を詰め込めばいいのでは?と思ったものの、それよりはデータ量を減らす方がいいだろうなと思い放置。
12:30 SQLiteにindex
12:40 1つのSQLiteファイルにマージ後を見越した改善
- pprofを見ると基本的に
sqlx.GetConnectが時間を食っている事がわかる。メインの方針は変わらず。-
GetConnectはscanAny等の別関数を呼び出していて、そこに時間がかかっている。名前通りconnectionを貼るのに時間がかかっているわけではないっぽい
-
- @__math: tenantDBを1つにmergeした前提のコードを書き始める github.com
13:38 visit_historyの削減
visit_historyの不要なレコードを生成しないように。また、不要なレコードの削除も- 未だにsqliteのmergeは終わらず。
player_scoreのデータを大幅に減らせば移行が一瞬で終わりそうという話を伝えて @chibieggに丸投げする。 github.com
13:49 sqlite内のデータの削減
14:03 MySQLへ移行
- レコード数が減ったので、 sqlite -> MySQL の移行も一瞬で終わる。 github.com 現在の構成は
ベンチを回すとそれぞれのCPU使用率が 100, 200, 150% 程度。tenantDBのCPUがボトルネックである。
14:49 N+1の解消
competitionRankingHandlerのN+1を解消する。 github.com
14:58 flockをDBMSのトランザクションに (40000+)
- ファイルを使ったトランザクションを消す。これで4万点。 CPUがボトルネックだったのでは…?と思ったけど、 N+1の解消で事情が変わった可能性が? github.com
既に予選突破が見えてきているので、あまりチャレンジャーな事をしないように意識し始める。
15:30 rankingのクエリ最適化
- @__math : INSERT時にrankingを作れば
limit 100 offset ?が消せるので、これと適切なindexを合わせて負荷軽減。 github.com - @ misodengaku :
playerHandlerのN+1を消してもらう github.com github.com
16:10 retry-after による負荷コントロール
- たまに500が返ってきて スコア-10%を喰らい始めたので
competitionsAddHandlerで 429 Retry-After を返すようにお願いする。- 負荷を見ながら429を返す実装は難しいので、10%の確率で429を返すようにした。 github.com
- @misodengaku にはmysqlの設定の調整をしてもらう
- 予選通過と予選一位のどっちがいいかという話で、守りに入りましょうという結論になる。
16:58 一部をインメモリに
- @chibiegg,@__mathで
playerやplayer_scoreをキャッシュするように改造。終わってから思ったんですけど、これは守りに入ったチームの戦略なのだろうか。 50000くらい出始める。 github.com github.com github.com
17:01 INSERTの完了を待たずにOKを返す (50000+)
- 最後に @__mathが
visit_historyのINSERTを非同期に github.com
17:05 再起動テスト
- 再起動試験を始める
- @misodengakuと@chibieggがログの出力の抑制、systemdの見直し
- その後全員で再起動後のテスト、DBが立ち上がるのが遅い場合にちゃんと動くかの確認などをする。 github.com
再起動テスト中に52957点が出る。あんまり高い点数が出て85%ルールに引っかかるとつらいので、ここでベンチマークを終了する。
再起動テストも終了してお開きに。
おまけ
準備表のバグで度々1,2位を独占して何だか嬉しかった

ISUCON10で予選敗退した
予選敗退しました。 多分最高得点は開始4,5時間目の1600前後ですが、多くの結果がcancelledになっており、我々のアプリのバグがシミュレーターのバグなのかわかっていません。
やったこと
- MySQLのバージョンを確認。DESCとASCを混ぜたindexを作るもEXPLAINするとFileを使っていることを確認。どうやらMYSQL8.xではないと駄目らしいので -popularityをinsertして全部ASCでorder by 出来るように
- ChairとEstateでDBを分ける。1台目をgo app, 2台目をChair用MySQL, 3台目をEstate用MySQLに
- Search用にindexを山盛り作る
- 各low priceをcache
- Spatial Indexを入れるために MySQL 8.xを採用、その後 -popularityは削除
- range query (80 <= height && height < 150 みたいなの)を heightRangeId = xxx の形に出来るように,DBのデータを追加したり
- Nginx側でbotを弾く
やってないこと
- NazotteのN+1の削減
- Recommendの大量のor句の削減。工夫すれば and 2個だけになりますね
感想
ポジティブ
- 運営お疲れさまでした!頭が上がらない
- 問題は非常に面白かった。コードが簡潔にも関わらず工夫する点が多数。
ネガティブ
- シミュレーターとポータルが両方不安定で、途中質問ページにすらたどり着けなかった。我々のアプリは得点は出ているにも関わらずcancelled、という状態で中盤止まってしまい身動きが取れなかった。
- 10分間以上Runningのテストを2回ほどcancelしてもらっていたので、"cancelled"は運営が負荷軽減のため手動でcancelしていたものだと勘違い。質問するまでに時間がかかった。
- タイミング悪く質問が出来なかったり(質問ページが502)、cancelledの理由は我々側かシミュレーター側の問題かの質問の回答に時間がかかったり。何回かの質問の回答待ちで1時間以上はかかったかも
- 競技中のシミュレーターに対する信用度が6割程度しかなく(言い換えれば4割はシミュレーターがバグっていると疑っていた)、シミュレータのバグだと信じて改善を続けるか、ある程度ロールバックするかで滅茶苦茶悩んだ。ロールバックしてしまったがそのまま突き進むべきだった。理由は以下の文章 (http://isucon.net/archives/55007956.html より)
ベンチマーカーの不具合により、スコアが 0 点となってしまう、あるいは正常に終了しない事象が発生しておりました。そのため、競技終了後、本不具合を修正した上で運営にて全チームに対して追試を行いました。
- ロールバックしてほとんどスコアの上がらないものを一から直すより、最新のcancelされてしまうものを改善し続けた方が通過する可能性は高かったように思う
- 前半4時間が楽しかっただけに後半が本当に残念。実力が足りずに落ちたと実感出来れば反省も出来るのだが…
その他
- シミュレーターとポータルの安定性を向上してほしいとは思うものの、それだけのことを行う人的余裕はないのでは?この規模の運営って死ぬほど大変だよね?とも思っている。
- 競技参加者なのでどうしてもネガティブな部分が具体的になって長めになっているが、毎年面白い大会を開催してくれている運営の人々に感謝しています
DDCC2019で準優勝した
DDCC2019という DISCOさん主催のオンサイトコンテストに参加しました。
コード部門 (10:10:00 開始)
A - レース (Race) (10:24:48 AC)
S において、- は必ず別の - と隣接して現れる と太字で書かれているのに見逃して、一般の場合を解いていた。
14分ちょっとでAC
B - 大吉数列 (Array of Fortune) (10:31:17 AC)
こういう問題は辞書順と同じく、現在見ている場所に x を置いて、無理なら別のものを置くというのを
先頭から貪欲に繰り返せば解けることが多い。
O(n2)では通らないが、明らかに残っているものの中で最大の数と最小の数以外を考えなくてもいいことが分かるのでO(n)で出来る。
- {1,2,3, ... N} の K転倒数 (転倒数の定義から察してください) は 0 で最小
- {N, N-1, ... 3, 2, 1} の K転倒数 (転倒数の定義から察してください) は N-K + N-K-1 + N-K-2 + ... + 1 + 0 で最大
- 上手に構築すれば 上記の単純な足し算の式からいくつかの数を抜き出すことが可能
- 例えば N=5, K = 2 の時、 {5,4,3,2,1} の K転倒数は 1 + 2 + 3 = 6 だが、ここから1と3を消して 2 だけにするとか 1だけ消して2+3 = 5にするとかは自由に出来る
- {a1, a2, ... ai-1} まで構築済みの時、aiの候補として、残っているものの中で最大の数と最小の数のみを考えれば上記の式でやれるよね
という感じになのだが、自分の頭の中では逆順に思いついていった。5が最初に出てくるのは経験だと思います。
Aで複雑な解き方をした分Bの方が簡単だった。
C - 光の反射 (Reflection of Light) (提出なし)
幾何は失敗すると時間が解けるので後回し決定。BをACした時点でDを解いている人もいるしDに突撃。
D - DISCO! (10:47:03 AC)
DPの遷移をSegment Treeに乗せると解けるやつということが分かるので実装する。個人的には一番簡単だった。類題はcodeforcesとかhackerrank, codechefで見かけるイメージ。
実行時間が13sと長いもののSeg木にvector<vector
CとEを見比べたところ、面白そうだしワンチャンあるのでEにチャレンジすることに。
E - 飾りつけ (Decoration) (12:02:42 AC)
- 1 ~ 2000 を 1~1000, 1001 ~ 2000 に分けるといいのか?(10:50)
- 上の分け方も2の累乗パターンは無理そう (11:00)
- 1 - 50 - 50 - 1 みたいなグラフを作れば 50 * 50 の値を表現出来そうだけどACは取れそうにない (11:10)
- 解説にある解法 #1 と同じです
- 結局の所 {a, a+1}, {b, b+1} みたいなのを1つのノードに集約出来なければこれ以上のノードは節約出来ない… (11:15)
- a を入力すると {a, a+1} を出力するような部分グラフは作れるっぽい (11:20)
- 1 ~ 2000 の数が与えられるんだから、{1,2}, {3,4}, {5,6}, ... {1999, 2000} みたいに分けて、{}, {a}, {a + 1}, {a, a+1} の4パターンに分けてどうにかする?どうにかって何?
- {a}と{a+1} は同一視していい
- 3つ, 4つ区切りでも出来そうだから、とりあえずノードの減りそうな3つ区切りにする
- {a}, {a, a+1}, {a, a+2}, {a, a+1, a+2} の 4パターンを考えればいいっぽい (11:30)
- こんがらがってきたので整理すると、こんな感じになる
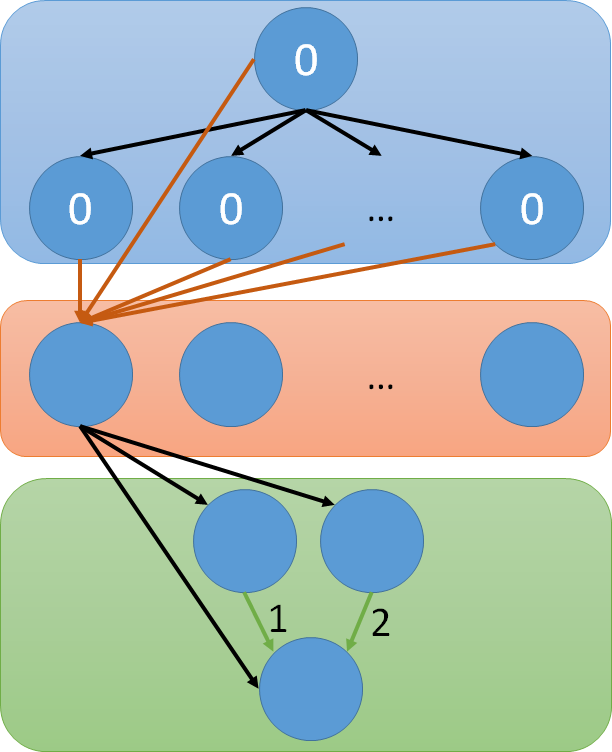
- 青い層で 0 を増やして、 青とオレンジの層の間で直積をとる感じで必要な数を生成。最後にオレンジと緑の層で {a}, {a, a+1}, {a, a+2}, {a, a+1, a+2} の生成を調整する。
- 最後の層のノードは3つ固定だが青とオレンジは分からない。解説にもあるように {a} パターンと {a, a+1} パターンは同じオレンジ層のノードに乗せることは出来ない。
- ノード数の合計は100以下なので、 青い層のノード数を i, オレンジ層のノード数を j として、答えを生成出来る中で i + j が最小のものを探せばいいのでは?
- 実装して出すと1080点 (11:55)
- 4つ毎に分ければどうなるだろう?ということでリファクタリングと改造を施しつつ粘る。
- AC!!! (12:02)
- これが駄目なら5つ毎パターン、参照のないノードの削除、オレンジ層と緑層の頂点の一部をマージするなどを考えていたが不要だった。
- ちなみに5つのパターンだと1140点らしい https://atcoder.jp/contests/ddcc2019-final/submissions/4060405
7, 8分でCが実装出来るはずもないので終了。結果は2位でした。
装置実装部門
MM形式にも関わらず予選が30分なので、読解&シンプル解法高速実装コンテストということが想像できる。
20分程度で書き上げたもののWA、最後までWAが取れなかった、残念。機械を範囲外に動かしたのが敗因だった様子。
装置部門の決勝がめちゃくちゃ楽しかったので次回参加出来れば勝ち上がりたい。
感想等
ICPCやISUCON, CTFだとそこそこの順位は何度も経験しているがこれらは全て団体競技。味方が強ければ、例え優勝出来たとしても自分単体はそこまで強いわけではないのかもしれないという気持ちが拭えなかった。 今回の個人大会では多数の強い人々が参加している中での2位なので本当に嬉しい。これまで参加していた大会の中でも一番かもしれない。
社会人となってしばらく経ち勉強や練習出来る時間も減ってしまった(スプラトゥーンが多大な影響を及ぼしている)。 同時期に競プロをしていた人々と同じようにそのうちゆっくりとフェードアウトしていくかもしれないが、いい思い出になった。
競プロが出来なくなる前に、ゆったりと参加出来て健康に良いらしいとされているKaggleにも参加してみたいですね。
帰る時にプレートも一緒に持って帰ろうかと思ったけど、冷静に考えると置く場所に困りそうなのでかわりに写真を撮っていただくことにした。快く引き受けてくださったスタッフの皆さんありがとうございました。
やったぜ pic.twitter.com/RDTf74ci5F
— まーす (@__math) 2019年1月19日
ISUCON8で準優勝した
大体はchibieggが書いてくれているので落ち穂拾いです ISUCON8で準優勝しました « chibiegg日誌
ISUCON8の決勝で準優勝しました、優勝できず非常に悔しかったです。 競技終了直前では50,000点を超えていたものの、再起動後のチェックで31,000点程度と大幅に下げてしまいました。
メンバーと担当は予選と変わらず
- chibiegg: インフラとコード
- misodengaku: インフラとコード、エスパー
- __math: コード
本戦のrepoはこちら、コミットログは例の如く雑です、8時間しか使われないので… github.com
時系列順
10:00
chibieggがansibleを書いている、sshの設定とかをしているようだが問題が公開されたので見る。
マニュアルが結構長い。misodengakuと同時に読み始めて、マニュアルを読み次第goのコードを読み始める。
SNSで拡散という項目をマニュアルでもコードでも見つけるが忘れる。
11:00 まで
とりあえずベンチマークを走らせてもらう、500点前後?
MySQLのslow logとnginxのアクセスログを出してもらう。
/info, /orders へのアクセスが大半の様子。
CPUは200%ガッツリ使っている。
帯域を頑張る問題には見えない。
流石に本戦でオンメモリ戦略をやるのはしんどいだろうということでMySQLは引き続き使うことにする。
DBとアプリケーションサーバを分離してもらう (misodengaku, chibiegg)
そうしている間にあからさまにLIMIT 1が必要なコードを見つけたのでつける。
ベンチを回すとそれだけで 5,000 点出る
12:00 まで
Sequel proをMySQLの本番環境に繋げると落ちて辛い。MySQLのバージョンが新しすぎて安定版では繋がらないのだろうという話になり、Sequel proの最新buildを使ってみると無事繋がる。
/info が支配的であることはわかる。ロウソクチャートを作るためのSQLが重たい事はわかるので、計算の仕方をちゃんと理解し始める。
理解が甘いまま高速化を始めたのでここでどうでもいいpull requestを出し始める
- add sec,min,hou by chibiegg · Pull Request #7 · chibiegg/isucon8-final-app · GitHub
- add indexes by chibiegg · Pull Request #9 · chibiegg/isucon8-final-app · GitHub
秒、分、時間チャートの情報を出すSQLのGROUP BYをしやすくするために CreatedAt だけではなく CreatedAtSec, CreatedAtMin, CreatedAtHou を追加している。
ちゃんとコードを読むと分かるのだがそこはボトルネックではない。
途中で気づいたものの、害はないのでそのままマージすることにする。
ここでEXPLAINした時にtableがpartitioningされていることに気づくがスルーする。実際はここでスルーすべきではなかった。
isucon.net 講評にかいてあるので詳細はこちらをどうぞ。
13:00 まで
なんか分からないけどGoLand上でisucoinが動かない、listenはしているようだが全てのリクエストにたいして404を返している様子。パソコンが何もわからない…
最終的にはロードバランシングが必要でしょうということでchibieggが準備し始める。
この時点でサーバ01でNginx+App、サーバ02でMySQL、サーバ03と04でApp、という構成に。
ただし、Initializeが全台に対して行われるための仕組みを作っていなかったので、いつでもロードバランスできる状態にはしておきつつ、一旦サーバ01だけで処理するようにしておきました。
ローソクチャート以外に他の人にやってもらえる作業としてisuloggerのbulk requestを挙げた、間違いなく8時間以内に上限に引っかかるので、今やっても後でやっても変わらない。(chibieggにしてもらう) 結果6,000点になった。
14:00 まで
なんか分からないけどGoLand上でisucoinが動かない、listenはしているようだが全てのリクエストにたいして404を返している様子。パソコンが何もわからない…(再)
もう諦めてGoLandはただのエディタとして扱う事を心に決める、結果本番環境以外無くなって構成がスッキリしたと前向きに捉える。
- 初期化を全ノードに実行できる準備 #11
- ロードバランスを再度有効化 #12
ベンチマーカーは実行開始前に一度だけ /initialize を実行します。
ロードバランスするとこの初期化リクエストは1つのアプリケーションプロセスにのみ届きます。
その時点で、全てのアプリケーションプロセスを初期化する必要があるため、内部APIを用意し (/internalInitialize) 全てのサーバの初期化を行うように実装しました。
また、設定をsettingテーブルから都度参照するようになっていたのをやめ、グローバル変数に持つように改修することでDBへのアクセスを減らしています。
ちゃんと動作はするようになったものの、数百程度のスコア上昇しかおきませんでした。
大体書いて、何故か手元で動かないので本番でchibiegg達にdebug、bug fixしてもらう。
その間暇なのでuser tableを見ていたら不要なlockがあるので消す。
15:00 まで
そういえばそんなものがあった気がしてきた、MySQL, Go App ともに負荷が少なくて不思議に思っていたところだった。
あまりにもtrueを返しすぎると、ユーザー増加に耐えられずタイムアウトが増えてしまうので、とりあえず1/8の確率でtrueを返すようにする。
16:00 まで
実装が重たそうなので敬遠していたが、どうしても必要に見えたのでローソクチャートのキャッシュに着手した。
雑じゃないロウソク足のキャッシュ by chibiegg · Pull Request #16 · chibiegg/isucon8-final-app · GitHub
特にバグも無く動作したとchibieggは書いているが、コミットログを見ると、きちんとバグっていたので2回bug fixをコミットしていることが分かる。
雑な /info キャッシュ #15 雑じゃないロウソク足のキャッシュ #16
ローソク足は、直近のものは変化するが過去のものは変化しない ローソク足は、秒単位で更新されれば良い という性質もと、私が雑にレスポンス丸ごとメモリにキャッシュする実装、まーす先生が丁寧にロウソク足をメモリにキャッシュする方法をそれぞれ実装しました。
私の雑なキャッシュでも特に問題はなく、一気に25000点弱に。
まーす先生の丁寧なキャッシュもバグ無く動作したため、両方をマージしました。
これがちゃんと動いたので /order の RunTrade に手を入れ始める。とりあえず不要なロジックを消すと 30,000点弱になる。 remove some checks by chibiegg · Pull Request #18 · chibiegg/isucon8-final-app · GitHub
編集がコンフリクトしないであろうUserのアプリケーション側でのキャッシュをchibieggにお願いする。
多少改善したがやはりRunTradeのSQLが重たそうに見える。なんとなくだがRunTradeが走った回数と約定が発生した回数に大きな開きがあるのではと感じ始める。 実際にログを仕込んだところ、精々10%ほどしか実際に約定処理が行われていないことがわかった。
このあたりでGo Appのプロファイリングを行ったところ99%がbcryptの処理であることが分かった(もう少し早めにプロファイリングをするべきかもしれない…?)
bcryptを外すと怒られるのでbcryptのコスト(回数)を10から4に落としたものの大差なし。ISUCON8の講評にはこれが効くと書いてあるが… おそらく/orderか/infoの方がボトルネックだった為効果を実感出来なかった…?
17:00 まで
ユーザーの情報をメモリにキャッシュの実装(chibiegg)が終わって30,000点を超える
RunTradeは /orderのPost requestとは別に行うようにしたところ 37,000点程に上昇する。
17:30 まで
ここまで終わったところ、どうも/orderの高速化は頭打ちで/infoのアクセス回数も多いことからなんとかならないかと頭を捻る。
正直やりたくなかったのだが 最低売却/最高購入価格のキャッシュを入れたところ 50,000点を超える。 1秒キャッシュしてもよかったのか…
18:00 まで
ようやく再起動テストを始める。アプリに問題が発生する要素はないのでMySQLの対策。 MySQLを再起動するたびに35,000~40,000点になるのでMySQLを温めるコードをchibieggが書く。 実際にサーバーの再起動して確かめる時間は無かったのでこれは行わず。しかし実際はサーバー再起動が大きく影響を与えたようで、結果論になるがこちらに力を入れるべきだった。
結果
30,000点程度に落ちて2位、無念。 MySQLを温めるスクリプトが足りていないだけでなく、MySQLの使うファイルがキャッシュに乗っていないのが大打撃となった模様。
感想
勝てなかった。もう少しちゃんとしていれば100,000点は本番中でも超えられたと思うので無念。
POST /signin のBanは実装していなかったがこれも実装すべきだった。
講評より
一方、競技時間中に最大スコアを記録し、惜しくも2位となった「takedashi」は上記で言うところの完全クリアまでたどり着いているようでした。
しかし、再起動試験においてエラーが多発し、1度目はtimeout多発によるfail、2度目はstatus codeが400で返ってくるという事態が発生し減点により結果を伸ばすことができませんでした。(htmlが返ってきていたのでアプリケーションの問題ではなさそうということしか原因はわかりませんでした。)
rebootによる再起動試験をしていたら、もしかしたら競技時間中に気づくことができたかもしれませんが、気づいたとしても対策できるような問題でも無い気がしますので、これもまたISUCONの面白さではないでしょうか?
"気づいたとしても対策できるような問題でも無い気がします" の部分に同意します。 取れる対策としてはもっと点数を上げることでしょうか…? 100,000点を超えていればエラー多発でも完走すれば50,000点は出ていただろうと思います。
またこちらも結果論ですが、userのbcrypt以外はmySQLは不要な問題だったと思うので、ISUCON名物のオンメモリ戦略を取るべきだったかなとも少し思っています。
ISUCON8予選をオンメモリ戦略で通過した
ISUCON8の予選に参加しました。運営の皆様お疲れ様でした、今年はオーソドックスな問題だった気がします。 isucon.net
結果 44,295点で全体8位、予選通過のようです。今年もよろしくお願いします。
メンバー
- chibiegg: インフラとコード
- misodengaku: インフラとコード
- __math: コード
- aki33524: 3人しか出れないので不参加 最近は太刀魚を釣っているらしい
死後硬直で曲がっとるがタチウオ pic.twitter.com/wzfiEsVdFk
— きひろちゃん@わたモテ百合はいいぞ (@aki33524) 2018年9月17日
以下箇条書き
- Goは速いだろうということでGoを選択。pythonの方が慣れているがCPU勝負になったときに不利…
- MacbookにGolandを入れていたが、Debuggerが起動せずに苦しんだ。なんか色々インストールする必要があるらしいが時間がないのでDebuggerなしでやることに
- Goのアプリのプロファイリング用にpprofというものがあるらしい、でも結局使わず
- misodengakuはリモートで参加。こちらの通話のみ聞こえており、misodengaku側がslackでのみ反応
競技開始
- パスワードでログインは面倒なので各サーバーにpublic keyを置いてもらう
- gitリポジトリを用意してもらう。GoのコードとDB初期化のコードはここで管理
- トイレに行って閉め出される、一回休み
- リバースプロキシはh2o、nginxじゃないの
- misodengaku, chibiegg がよしなにしてくれた
- アプリはGo + MySQLのシンプルなもの。フロントはjsで触るところはなかった。APIと何個かのhtmlを返すエンドポイントをいい感じにする
- 取りあえずベンチマークを走らせる。
09/16 10:18:47 レスポンスが遅いため負荷レベルを上げられませんでした。/ 09/16 10:18:48 レスポンスが遅いため負荷レベルを上げられませんでした。/ 09/16 10:18:49 レスポンスが遅いため負荷レベルを上げられませんでした。/ 09/16 10:18:50 レスポンスが遅いため負荷レベルを上げられませんでした。/ 09/16 10:18:51 レスポンスが遅いため負荷レベルを上げられませんでした。/ 09/16 10:18:52 レスポンスが遅いため負荷レベルを上げられませんでした。/ 09/16 10:18:53 レスポンスが遅いため負荷レベルを上げられませんでした。/ ...
- "/" が遅いらしい サーバの負荷は
PID USER PR NI VIRT RES SHR S %CPU %MEM TIME+ COMMAND 7525 mysql 20 0 1633596 260344 9480 S 77.7 25.6 1:56.13 mysqld 7784 isucon 20 0 268432 145580 4720 R 31.3 14.3 0:38.41 torb
- とりあえずmysqlがネックらしい?コードを読む
- エンドポイントを洗い出す
- "/admin/" 以下になんかある?"/"以下と同じくらいの実装量のページ?
- table多い
- "/"がすごい量のSQLを吐き出している。localのGo + 本番サーバー上のMySQLで動かすとなんとレスポンスに40s+かかる。明らかにクエリを減らす必要がある
- ssh -L でトンネルを作って接続していた。全てのdev環境が本番DBを参照する素敵仕様
- ついでにサーバのスペック確認してもらう
CPU: 2 メモリ : 1GB
- メモリ少ないっぽい
- MySQLとGoがCPU/Memoryを食べあうことになりそうなので早めに分離。
アプリケーションサーバを3、DBを1にしました
misodengaku [11:12 AM] slowlog的にはここで全件取ってそうでやばそうぐらいしか見えない
e.GET("/admin/api/reports/sales", func(c echo.Context) error { rows, err := db.Query("select r.*, s.rank as sheet_rank, s.num as sheet_num, s.price as sheet_price, e.id as event_id, e.price as event_price from reservations r inner join sheets s on s.id = r.sheet_id inner join events e on e.id = r.event_id order by reserved_at asc for update")chibiegg [11:14 AM] リクエスト的には GET / GET /api/events/10 GET /admin/ POST /api/events/11/actions/reserve が重い (合計時間的な意味で)
- MySQLに格納されているデータを見る。
- INSERT/UPDATEのないテーブルは起動時にメモリに載せればいいよね
sheetsはもうちょっとなんとかなるでしょ- …ていうか全部合わせても100MBいかなくない?
- 基本全部Go側でデータ持てば良くない?MySQLはデータの永続化にのみ使用して、起動時にデータ全読み込みでいいよね?
- 2018/09/17 追記 アプリケーションを1つしか起動しなくてもパフォーマンス十分出るよね?
- ISUCONだからね
- INSERT/UPDATEのないテーブルは改造するのに難しい点はない。半分がメモリ上のデータ、残り半分がSQL発行してデータ取得しててもベンチマークは通るし通らないとバグっていることがわかる
- 一方INSERT/UPDATEがある場合は結構複雑、色々考えたけど競技時間が8時間しかないということで以下の方針で行くことにした
reservationテーブルと例に上げると、
1. 起動時にDBから全reservationデータを取り出す
var ( reservationStore = make([]*Reservation, 0) reservationMutex = new(sync.Mutex) ) // main内と /initializeで呼ばれる func initReservation() error { rows, err := db.Query("SELECT * FROM reservations") if err != nil { return err } defer rows.Close() reservationStore = make([]*Reservation, 0) for rows.Next() { var reservation Reservation rows.Scan( &reservation.ID, &reservation.EventID, &reservation.SheetID, &reservation.UserID, &reservation.ReservedAt, &reservation.CanceledAt) reservationStore = append(reservationStore, &reservation) } return nil }
- SELECT/INSERT/UPDATEは全て
reservationStoreのデータを参照/追加/更新する - INSERT/UPDATEは、アプリ/マシンの再起動に備えてMySQLにもデータを流す。ただしアプリは起動時以外一切データを見ないので非同期でSQLを発行
// mutexで保護しつつ reservationStoreのデータを追加 go func() { res, err := db.Exec("INSERT INTO reservations (id, event_id, sheet_id, user_id, reserved_at) VALUES (?, ?, ?, ?, ?)", reservation.ID, reservation.EventID, reservation.SheetID, reservation.UserID, reservation.ReservedAt.Format("2006-01-02 15:04:05.000000")) if err != nil { log.Println("error happened on Exec") return } // 追加のエラーハンドリング }()
- メリット
- デメリット
event := eventStore[id]
// eventの更新
go func() {
// NG 実行されるgoroutineの順番によっては最新でないeventを元にしたUPDATEが発行される恐れがある
if _, err := db.Exec("UPDATE events SET public_fg = ?, closed_fg = ? WHERE id = ?", event.PublicFg, event.ClosedFg, event.ID); err != nil {
log.Println(err)
}
}()
- SAFE
// eventStoreの更新 go func() { // OK 実行されるgoroutineの順番によらず、最新の状態を元にUPDATEが発行される // どのeventStoreの更新よりの後に実行されるgoroutineは必ず一つ以上あるので、実行中にKillされない限りMySQL内のデータもいずれは最新の状態になる event, _ := getEvent(eventID, -1) if _, err := db.Exec("UPDATE events SET public_fg = ?, closed_fg = ? WHERE id = ?", event.PublicFg, event.ClosedFg, event.ID); err != nil { log.Println(err) } }()
ISUCON以外でやろうとすると怒られる。indexを貼ってもMySQLでパフォーマンスが満足できないなら次はRedisを試すのだろうか?
sheetはボトルネックではないけど、他の箇所の編集と競合しづらいだろうと考えchibieggに頼む- INSERTがあるけど、
reservationが減れば嬉しいだろうと考えてなんとかしようとする eventもでかいけど後回し- 11:30 くらいからみんなで着手し始めた
- このあたりでsheet関係のSQLが無くなったのでベンチマークを走らせたら"座席がランダムではありません"と怒られる。ランダムじゃないとだめなのか…
- Fisher-Yatesのシャッフルを実装したら通った。スコアは変わらず
- 13:30くらいになって
reservation周りの半分くらいSQLを消す。この時点で半分がメモリ上の情報のみを参照して残りがDBの情報を参照する - 残りの
reservationは私がして、chibieggとmisodengakuにuser周りをなんとかしてもらうことに - 多分14時くらい
getEventsが爆速になった(local 40s -> 1s未満)のでlocalでのデバッグが捗る - 15:00 全部
reservation周りのSQLが全部消えたのでテストするけどfailする。多分UPDATEが悪さしてる - なんか
userもバグってるらしい。reservationの方が動かないとスコアは上がらないのでchibieggにdebugを頼む - INSERT時にMutexで保護する範囲を広げたり色々直す
- 15:34 30000点を超えて1位になったので喜ぶ
- Goがだいぶ分かってきたのでこの調子で
eventも剥がすことに。次のボトルネックを探してた気がするけど何だったか忘れてしまった - gzipで圧縮してみたら?ってことでやったらスコアが下がる
- 16:47
eventを剥がし終わったのでもっかいベンチを走らせるも25000点。topで見るとCPUを使い切っている - どうせ帯域は余裕があるしgzipを切る
- 40000点を超える
- CPUがボトルネックだしh2oも別サーバに移動で良くない?
- そんなに変わらない
- そろそろ残り1時間ちょっとだし、予選は突破できそうなのでベンチガチャを開始することに
- 17:14 最高得点(44295)が出る。何も変えてないのに2万点弱ブレてびっくりする
- 目標は予選突破であって1位ではないのでこれで撤収。ホワイトなISUCONだった
感想
- MySQLからデータを剥がしてスコアが上がるのは面白い、結局今回はindexを使わなかった気がする
- ちゃんとindexを貼ってもスコアは上がったらしい?こっちの戦略でも良かったかな…
- プロファイリングが必要な段階まで行けなかったのは心残り
- データ全部剥がした後適切なデータ構造で管理すればスコアは軽く倍になりそう。20万の
reservationを愚直に回しまくっていたのが問題
- データ全部剥がした後適切なデータ構造で管理すればスコアは軽く倍になりそう。20万の
From(reservationStore).Where(func(c interface{}) bool { r := c.(*Reservation) if r.EventID != event.ID { return false } if r.CanceledAt != nil { return false } return true }).ToSlice(&reservations)
- Goでlinq辛すぎ問題。interface{}何回出てくるんだ…
SELECT event_id FROM reservations WHERE user_id = ? GROUP BY event_id ORDER BY MAX(IFNULL(canceled_at, reserved_at)) DESC LIMIT 5
- After
From(relatedReservations).GroupBy(func(c interface{}) interface{}{ r := c.(*Reservation) return r.EventID }, func(c interface{}) interface{} { return c }).OrderByDescending(func(c interface{}) interface{} { values := c.(Group).Group maxTime := From(values).Select(func(c2 interface{}) interface{} { r := c2.(*Reservation) if r.CanceledAt != nil { return r.CanceledAt.UnixNano() } else { return r.ReservedAt.UnixNano() } }).Max().(int64) return maxTime }).Take(5).Select(func(c interface{}) interface{} { eventId := c.(Group).Key return eventId }).ToSlice(&eventIds)
- 普段使わないlaptopで苦戦した。IDEのインストールとかは事前にするとよさそう
- branch名を間違えてreserveのつもりがreverseになっていた。英語…
- 面白かったです
Størmerの定理
前書き
$2^{n} - 3^{k} = 1$ を満たす正の整数 $(n,k)$ をすべて求めなさい。
いきなりですが、上記の問題が解けるでしょうか?
まず小さい数を代入していくと、$(n,k) = (2,1)$ の時は $2^{2} - 3^{1} = 1$ となってこれを満たすことがわかります。 それ以外の解は見つかるでしょうか? 何となく無さそうですが確証は持てないですね…
こういう問題は 指数型の不定方程式 とか呼ばれているそうです。受験で出てきそうな見た目をしていますが、この問題は凶悪なのか解法は見たことがないです。 この問題、解きたいですよね?
今回は Størmerの定理(Stormerの定理) と呼ばれている定理を用いて、$2^{n} - 3^{k} = 1$ を満たす正の整数 は $(n,k) = (2,1)$ のみであることを証明します。
今回の証明は http://kam.mff.cuni.cz/~klazar/stormer.pdf を要約したものとなっています。
続きを読むWindowsで、実行ファイルを書き換えずに既存の.Netアプリケーションのメソッドを置き換える話
動機
昔、箱庭XSSという問題がSECCONで出題されました。 どのような問題だったかは他の方のブログを見て頂ければ分かるかと思います。
問題作者のスライドはこちらです。
【XSS Bonsai】 受賞のご挨拶 by @ymzkei5 【SECCON 2014】 - Dec 08, 2014
このアプリケーションは.Net製で、
- 難読化
- 既存のdecompilerでは C#, VB.Netのコードに変換出来ない(大体落ちたり例外が発生する)
- デバッガでattachすると挙動が変わったり、答えが変わる
- バイナリを書き換えると、checksum一致処理に引っかかる
という特性があります。
webの問題として解いてほしいらしく、作者さんのスライド曰く

とのことなので、チートで解こうと考えました。
今回要求される要件は
- debugger検知に引っかからない
- 実行ファイルを書き換えない
- checksumが変わるため
の二つです。
disassembleしてみると、「正規表現で文字列を置換している処理さえ潰せればフラグを取れるのでは?」と思ったので、「Regex.Replaceの挙動を変更する」ことを目標にしました。
しかし箱庭XSSのみに特化したプログラムを書いても面白くないので、もうちょっと大きく出て「.Netアプリケーションのメソッドを、実行ファイルを書き換えずに挙動を変える」ということにしましょう。
(なおこれ以降箱庭XSSは出てきません、手段と目的は往々にして入れ替わります)
実装
に置いてあるのでご自由にどうぞ。(英語でコメント書こうとして挫折した後がありますね) とりあえず試してみたい人は https://github.com/math314/DotNetInjection/releases/tag/v1.0 から Release.zip をダウンロードして試してみてください。動かし方はreadmeに書いてあります。
続きを読む