前置き

これは、Competitive Programming Advent Calendar Div2013, 第 13 日の記事です。

みんな大好き期待値の問題の基礎について確率変数を使わない縛りで書きたいと思います。

1,2は非常に簡単な内容となっているので読み飛ばしても構いません。

1. サイコロの目の期待値

1から6の目が書いてあるサイコロがある。
どの面も出る確率が1/6の時、出る目の期待値Eを求めよ。

出る目と確率はそれぞれ

目	1	2	3	4	5	6
確率	1/6	1/6	1/6	1/6	1/6	1/6

となるので、期待値は \[ (1 + 2 + 3 + 4 + 5 + 6) * \frac{1}{6} = \frac{7}{2} \] となります。答えは \( E = \frac{7}{2} \) これは簡単ですね。

類題

AtCoder Beginner Contest #003 A AtCoder社の給料

この記事を書いている時に atcoderで出題されました、びっくり。

2. 二つのサイコロの目の和の期待値

1から6の目が書いてあるサイコロが2つある。
どの面も出る確率が1/6の時、出る目の和の期待値Eを求めよ。

愚直解

出る目とその確率は以下の様になる。

	1	2	3	4	5	6
1	1/36	1/36	1/36	1/36	1/36	1/36
2	1/36	1/36	1/36	1/36	1/36	1/36
3	1/36	1/36	1/36	1/36	1/36	1/36
4	1/36	1/36	1/36	1/36	1/36	1/36
5	1/36	1/36	1/36	1/36	1/36	1/36
6	1/36	1/36	1/36	1/36	1/36	1/36

よって答えは、\[ ( (1+1) + (1+2) + (1+3) + ... +(6+3) + (6+4) + (6+5) + (6+6) ) * \frac{1}{36} = 7 \] より、 \( E = 7 \) となります。しかし明らかにもっと効率の良い計算方法がありますね。

条件付き期待値

1つ目のサイコロを振ったところ k が出た。
この時2つのサイコロの目の期待値は？

目の出方は(k,1),(k,2),(k,3),(k,4),(k,5),(k,6) の6通りで、それぞれ確率は1/6です。よって期待値は、 \[ (k + 1 + k + 2 + k + 3 + k + 4 + k + 5 + k + 6) * \frac{1}{6} = k + \frac{7}{2} \tag{1} \] となります。

この(1)を1つ目のサイコロの目がkの時の条件付き期待値と言います。

さて,1つ目のサイコロでk (= 1,2,3,4,5,6)が出る確率はそれぞれ 1/6 なので、求めたい答えEは、 \[ E = \sum_{k = 1}^6 (k + \frac{7}{2}) * \frac{1}{6} = 7 \] となります。

このように、\[ (期待値) = \sum (条件付き期待値) * (その条件となる確率) \] が一般に成り立ちます。この式は非常に重要で、以下バンバン出て来ます。

3. コイントス

表裏がそれぞれ 1/2 で出るコインを投げる。
初めて表が出るまでに投げる回数の期待値Eは？

解法1

高校数学の試験でありそうな解答です。

i回目に初めて表が出る確率を\( p_i \) とすると、\( p_i = \frac{1}{2}^i \) となります。期待値Eは、 \[ E = \sum_{i = 1}^{\infty} i * p_i \] より、 \[ E = 1 * \frac{1}{2} + 2 * \frac{1}{4} + 3 * \frac{1}{8} + ... \tag{2} \] (2) * 2は \[ 2*E = 1 * \frac{1}{1} + 2 * \frac{1}{2} + 2 * \frac{1}{4} + ... \tag{3} \] となり、 (3) - (2) を計算すると

\[ 2*E - E = 1 + \sum_{i = 1}^{\infty} \frac{1}{2}^i = 2 \] 以上から \( E = 2 \) と分かりました。

解法2

条件付き確率を使って解きます。

1回目に表が出た時、初めて表が出るまでに投げる回数の期待値は、明らかに1です。

じゃあ1回目に裏が出た時の期待値は？ \begin{align*} (1回目に裏が出た時の、初めて表が出る期待値) &= (2回目以降で初めて表が出る期待値) \\ &= 1 + (1回目以降で初めて表が出る期待値) \\ &= 1 + E. \end{align*} より、1 + Eとなります。

後は条件付き確率を用いて

\begin{align*} E &= 1 * \frac{1}{2} + (1 + E) * \frac{1}{2} \\ &= 1 + \frac{1}{2} * E \\ E &= 2. \end{align*}

と計算出来ます。解法1より簡単！(なはず)

これを図で表すと以下のようになります。

f:id:math314:20131213190207p:plain

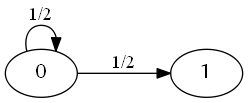
図の数字が、何回連続で表が出たかに対応しています。 1から辺が伸びていないのは、1回でも表が出たら試行がそこで終了するからです。

4. コイントス2

表裏がそれぞれ 1/2 で出るコインを投げる。
初めて3回連続で表が出るまでに投げる回数の期待値Eは？

の解法1の様に式を立てるとどうなるでしょう？ i回目で、表がk回連続で出る確率を \( p_{i,k} \) とします、ただし、k = 3は、初めて3回連続で出る確率とします。

これを図で表すと以下のようになります。

f:id:math314:20131213033148p:plain

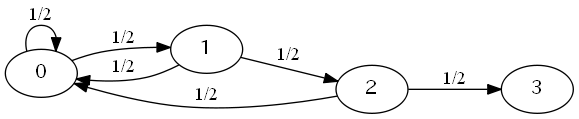
3から辺が伸びていないのは、前の図と同様の理屈で、3回連続で表が出たら試行がそこで終了するからです。

条件から以下の連立方程式が成り立ちます。

\begin{align*} p_{i+1,0} &= (p_{i,0} + p_{i,1} + p_{i,2} ) / 2 \\ p_{i+1,1} &= p_{i,0} / 2 \\ p_{i+1,2} &= p_{i,1} / 2 \\ p_{i+1,3} &= p_{i,2} / 2 \end{align*}

後は、 \[ E = \sum_{i = 1}^{\infty} i * p_{i,3} \] を求めるだけですね！さて、やってみると分かると思いますが、 \(p_{i,3} \) の一般項を求めるのは非常に骨が折れます、4項間漸化式を解いて下さい、~~私は嫌です~~。

ここでも条件付き期待値が大活躍します。

解法1

1回目に表が出た時の期待値を \( E_f \)とします。対して1回目に裏が出た時の期待値は \(E_b \)とします。 \(f,b \) はそれぞれ表裏を表しています。

条件付き期待値から \[ E = E_{f} * \frac{1}{2} + E_{b} * \frac{1}{2} \tag{4} \]

さて、前回の結果から、\( E_b = 1 + E \) であることは分かっています。では \( E_f \) はどのように表されるでしょう？

1,2回目にそれぞれ表表と出た時の期待値を \(E_{ff} \),表裏と出た時の期待値を \(E_{fb} \)とすると、条件付き期待値より \(E_f \) はこの二つの変数を用いて \[ E_f = E_{ff} * \frac{1}{2} + E_{fb} * \frac{1}{2} \tag{5} \] と表されます。 \( E_b \) の議論から、\( E_{fb} = 2 + E \)だと分かります。

同様に考えれば \[ E_{ff} = E_{fff} * \frac{1}{2} + E_{ffb} * \frac{1}{2} \tag{6} \] が成り立つ事も分かると思います。同様に \( E_{ffb} = 3 + E \) です。また \( E_{fff} = 3 \) であることも分かります。

少しややこしいですが、以上の式から \( E \)を求める事が出来ます。

(4),(5),(6)より、 \begin{align*} E &= \frac{1}{2} * E_f + \frac{1}{2} * (1 + E) \\ E_f &= \frac{1}{2} * E_{ff} + \frac{1}{2} * (2 + E) \\ E_{ff} &= \frac{1}{2} * 3 + \frac{1}{2} * (3 + E) \\ \end{align*} 以上より \( E = 14 \) となります。

解法2

もう少し別の考え方も出来ます。 \( E_0,E_1,E_2,E_3 \) を、既に表が0,1,2,3回連続で出ている時に、追加で何回コインを投げれば終了するか？の期待値だとしましょう。

この添字は図の0,1,2,3と対応しています。

f:id:math314:20131213033148p:plain

また、求めたい期待値は、 \( E = E_0 \) です。

解法1と同様に考えていきましょう。まず \( E_0 \) です。

表が連続で0回、つまり裏が出た状態です。ここからコインを1回投げればどの状態になるか考えます。

コイン	状態
表	表が連続で1回出た状態
裏	表が連続で0回出た状態

となりますね。既にコインを1回投げた場合を考えているので、条件付き期待値から \[ E_0 = \frac{1}{2} * (1 + E_1) + \frac{1}{2} * (1 + E_0) \tag{7} \] となります。

\( (1 + E_1) \)は「0回連続表が出た状態から、1回目に表が出る場合に何回コインを投げればいいか」の期待値です。

同様に \( (1 + E_0) \) は「0回連続表が出た状態から、1回目に裏が出る場合に何回コインを投げればいいか」の期待値です。

この式は変形して \[ E_0 = 1 + \frac{1}{2} * E_1 + \frac{1}{2} * E_0 \tag{8} \] とも書けます。期待値問題の解説ではこの式が出てくる事が多いです。

この式は「\(E_0 \)から1回コインを投げると、1/2で\(E_1 \),1/2で \(E_0 \) へと移動する」を意味しています。残りの\( E_1,E_2,E_3 \) も同様の式展開をすると

\[ E_0 = 1 + \frac{1}{2} * E_1 + \frac{1}{2} * E_0 \tag{9} \] \[ E_1 = 1 + \frac{1}{2} * E_2 + \frac{1}{2} * E_0 \tag{10} \] \[ E_2 = 1 + \frac{1}{2} * E_3 + \frac{1}{2} * E_0 \tag{11} \] \[ E_3 = 0 \tag{11} \]

となります。解法1よりも見やすいと思います。

これをグラフと見比べてみると、

\( E_0 = 1 + \frac{1}{2} * E_1 + \frac{1}{2} * E_0 \)

f:id:math314:20131213192157p:plain

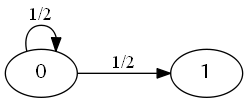
\( E_1 = 1 + \frac{1}{2} * E_2 + \frac{1}{2} * E_0 \)

f:id:math314:20131213192158p:plain

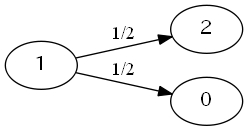
\( E_2 = 1 + \frac{1}{2} * E_3 + \frac{1}{2} * E_0 \)

f:id:math314:20131213192200p:plain

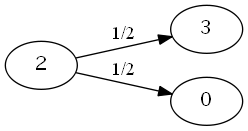
つまり、 状態遷移を表すグラフを作る事ができれば、期待値についての立式が出来ます！

注意

サイコロの目の和の様に、普通に計算した方が楽な場合があります。
立式出来ても解けるとは限りません、TLE,MLEの可能性もあります。

問題

TDPC J ボール
ARC016 C ソーシャルゲーム
ARC016 D 軍艦ゲーム
- 立式してから一工夫必要です、連立方程式を解こうとするとTLEすると思います。

まとめ

期待値の問題が分からなかったので解説を見たら、いきなり式が書いてあって「？？？」となったのがこの記事を書くきっかけです。なので何故その式が成り立つのかを丁寧に解説したつもりなのですが、わかりにくいところがあったら教えて下さい。

そういえばプログラミング要素も競技要素もない気がする。

興味がある人は、「コイントスをして初めてn回連続表が出るまでに投げる回数の期待値」も考えてみてください、紙と鉛筆で解けます。略解は反転。

\( E = (2^{n+1} - 2) \) 数学的帰納法で証明出来ます。

おまけ

マルコフ連鎖と吸収状態

マルコフ連鎖とは、マルコフ性(無記憶性)を持った確率過程の事です。ではマルコフ性は何か？というと、未来の状態が、過去の状態によらず現在の状態にのみ依存するという性質です。

例としてコイントスを考えます。

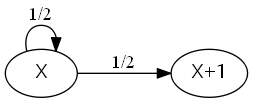
表裏がそれぞれ 1/2 で出るコインを投げる。
表なら点数に1を足し、裏なら何もしない。
n回投げた時の点数がXの時、n+1回目の点数はどうなるか

n回目での点数がXなので、n+1回目の点数はX,X+1のいずれかであり、確率はそれぞれ1/2と分かります。このように、n回目の状態だけでn+1回目の状態,確率を求められる事をマルコフ性といいます。

また、次の様に有向グラフでも表せます。矢印の上の確率は、遷移確率と呼ばれています。

f:id:math314:20131213205404p:plain

吸収的マルコフ連鎖と吸収状態

またコイントスを考えます。 4章と同じ問題です。

表裏がそれぞれ 1/2 で出るコインを投げる。
初めて3回連続で表が出るまでに投げる回数の期待値Eは？

この問題の有向グラフは次の様にも考えられます。

f:id:math314:20131213204604p:plain

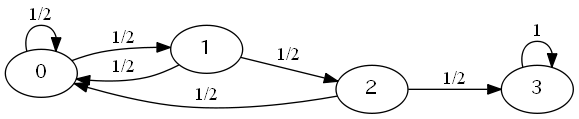
3の所にループが増えていますね。このように、別の状態に移動できない状態を吸収状態と呼びます。またこのように吸収状態を持ったマルコフ連鎖の事を吸収的マルコフ連鎖と呼びます。

吸収状態へ収束する期待値は、遷移確率行列を用いて簡単に計算出来ます。

http://sysplan.nams.kyushu-u.ac.jp/gen/edu/SystemsDesignEngineering/2006/kougi08/kougi08.pdf が参考になると思います。(逆行列の計算がO(n³)なので、競技プログラミングでは使う機会が少なそう)

MCMC : Marlov Chain Monte Carlo(マルコフ連鎖モンテカルロ法)

MCMCはサンプリング手法を意味しているんですが、これを最適化にも使うことが出来ます。それ、あるいはその1つがSA(焼きなまし法)です。

焼きなまし法については shindanninさんの焼きなまし法のコツが非常に分かりやすいと思います。

math314のブログ

主に競技プログラミング，CTFの結果を載せます

期待値と条件付確率

前置き